Как понимать язык статистики
Общей проблемой среди многих профессий является неспособность специалистов-практиков общаться со своими клиентами. Адвокаты часто виновны в том, что они говорят на юридическом языке с людьми, которых они представляют, не подозревая, что он им незнаком.
- Аналитика бизнеса
- Методы анализа данных Data Mining
- Как понимать язык статистики
Оглавление
Язык статистики
Общей проблемой среди многих профессий является неспособность специалистов-практиков общаться со своими клиентами. Адвокаты часто виновны в том, что они говорят на юридическом языке с людьми, которых они представляют, не подозревая, что он им незнаком. Врачи иногда борются одинаково, хотя их эффективность зависит от их способности четко общаться со своими пациентами. Статистики борются с этой проблемой больше, чем большинство. Вы можете быть самым продвинутым статистиком в мире, но если вы не можете четко сообщить о своих выводах лицам, принимающим решения, ваша работа теряется. Умение выражать статистические данные так, чтобы их могли понять не статистики, должно быть фундаментальным требованием статистической подготовки. Я подозреваю, что эта проблема часто возникает не из-за неспособности, а из-за недостатка осведомленности. Действительно трудно воздержаться от использования статистической речи, когда вы в ней свободно владеете, но я думаю, что большинство статистиков теряют понимание того факта, что другие не понимают этого, поэтому они редко даже пытаются преодолеть проблему. Решение этой проблемы начинается с осознания. Я буду использовать пример из работы талантливого статистика Говарда Вайнера, чтобы проиллюстрировать эту проблему и ее решение.
На внутренней стороне обложки новейшей книги Говарда Вейнера « Правда или правдивость» появляются слова: «Эта мудрая книга обязательна для чтения любому, кто когда-либо хотел оспорить высказывания авторитетных деятелей». Включая слово «правдивость» в названии – Слово, которое придумал комик Стивен Кольбер, – еще раз говорит о том, что предполагаемая аудитория Уэйнера широка; конечно, не ограничивается статистиками. В течение долгой и продуктивной карьеры Вайнер внес огромный вклад в области статистики и визуализации данных. Я многому научился по его книгам. Однако, читая их, я иногда сжимался в ответ на разделы, которые обычные читатели могут счесть запутанными или даже вводящими в заблуждение из-за недостатка статистической подготовки. Я нахожу это разочаровывающим, потому что я хочу, чтобы основные понятия статистики были более широко поняты. Я отмечаю тех редких статистиков, которым удается говорить о своем ремесле доступными способами. Чарльз Уилан, автор « Голой статистики» , и Нейт Сильвер, автор «Сигнала и шума» , являются двумя статистиками, которые не потеряли связь с миром в целом.
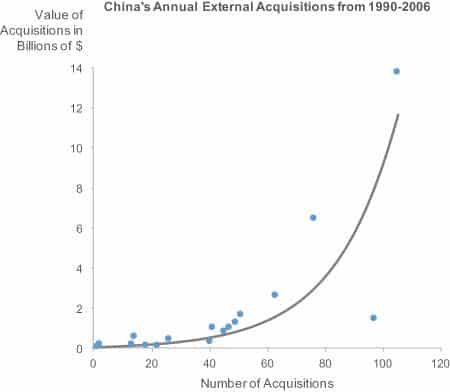
В « Правде или правде» Вайнер критикует график, появившийся в « Нью-Йорк Таймс», и изменяет его дизайн таким образом, чтобы, по его мнению, он был более эффективным. Вот оригинальный график:
Эта комбинация пузырькового графика и гистограммы рассказывает об увеличении числа приобретений Китая за пределами страны, как в количестве сделок, так и в стоимости этих сделок в миллионах долларов. Хотя Вайнер считает, что это может быть отображено более эффективно, как и я, он приписывает ему две положительные характеристики.
Сюжет New York Times о растущей заинтересованности Китая в этом состоит из двух вещей. Он содержит тридцать четыре точки данных, которые по стандартам средств массовой информации богаты данными, ярко демонстрируя сопутствующее увеличение в двух рядах данных за семнадцатилетний период … И, во-вторых, использование кругового представления Playfair позволяет увидеть расходы в течение более чем одного года. широкий масштаб
( Правда или Истина , Говард Уэйнер, издательство Кембриджского университета, 2016, стр. 105)
Хотя это правда, что New York Times лучше основывает свои истории на достаточном количестве данных, чем большинство новостных публикаций, я бы не назвал их использование пузырьков в верхней диаграмме удачным. Пузыри, которые кодируют значения, основанные на их областях, требуют меньшего вертикального пространства, чтобы показать этот широкий диапазон значений, чем столбцы, но это небольшое преимущество стирается из-за того, что люди не могут судить об относительных областях кругов легко и точно, и при этом они не могут легко сравнивать столбцы с пузырьками, чтобы четко видеть взаимосвязь между этими двумя переменными по мере их изменения во времени. Уэйнер отмечает, что использование пузырьков было введено Уильямом Плейфайром, великим пионером графической коммуникации, но Плейфэйр не воспользовался нашими знаниями о зрительном восприятии, когда он использовал эту технику. Статистики должны изучить, что работает перцептивно, как часть их обучения визуализации данных. Часть понимания вашей аудитории – это понимание того, как работает их мозг.
Давайте теперь посмотрим на альтернативный дисплей, который предлагает Wainer.
Прежде чем критиковать это сами, давайте послушаем, что говорит Вайнер.
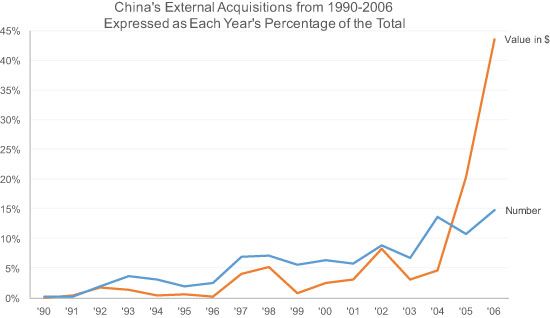
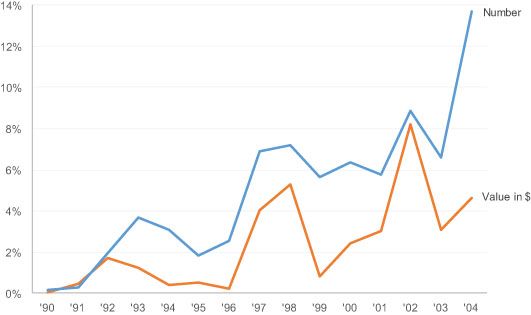
Могут ли другие альтернативы работать лучше? Может быть. На рисунке 9.14 показан двухпанельный дисплей, на котором каждая панель несет один из рядов данных. Панель 9.14a [верхняя панель] представляет собой простой разброс, показывающий линейное увеличение количества приобретений, совершенных Китаем за последние семнадцать лет. Наклон подобранной линии говорит нам о том, что за эти семнадцать лет Китай в среднем увеличил свои приобретения на 5,5 / год. Эта важная деталь отсутствует в последовательности столбцов, но очевидна из подгоночной линии регрессии на графике рассеяния. Панель 9.14b [нижняя панель] показывает увеличение денег, потраченных на приобретения за те же семнадцать лет. График представлен в логарифмическом масштабе, и его общая тенденция хорошо описывается прямой линией. Эта линия имеет наклон 0,12 в логарифмическом масштабе и, следовательно, означает увеличение примерно на 32 процента в год. Таким образом, тенденция, установленная в течение этих семнадцати лет, показывает, что Китай увеличивал количество активов, приобретаемых каждый год, а также приобретал все более дорогие активы.
Основное преимущество использования парных диаграмм рассеяния с линеаризованными преобразованиями и прямыми прямыми линиями заключается в том, что они обеспечивают количественную меру того, как изменилась доходность Китая. Это отличает график 9.14 от графика New York Times, который, хотя и содержал всю количественную информацию, необходимую для выполнения этих расчетов, в основном содержал качественное сообщение.
Диаграммы рассеяния Уэйнера и его объяснение включают в себя несколько предположений о знаниях своей аудитории, которые скучают по лодке. Даже если его читатели все понимают, как читать диаграммы рассеяния, диаграмма рассеяния не является хорошим выбором для этой информации. Очевидно, что центральной темой этой истории является то, как китайские приобретения менялись со временем, но это не так легко увидеть на графике рассеяния. Просто соединив значения в каждом графике с линией, шаблоны изменений во времени и их сравнения станут ясно видны.
О верхнем графике, говорит Вайнер,
Наклон подобранной линии говорит нам о том, что за эти семнадцать лет Китай в среднем увеличил свои приобретения на 5,5 / год. Эта важная деталь отсутствует в последовательности столбцов, но очевидна из подгоночной линии регрессии на графике рассеяния.
Это яркий пример отключения от мира в целом, от которого страдают многие статистики. Большинство людей не понимают значения наклона линии тренда на графике рассеяния, за исключением того факта, что в этом случае она имеет тенденцию к росту. Без аннотации, которую он включил в график, увеличение числа сделок в год на 5,5 в год оставалось бы неизвестным. Я также не думаю, что указание этого увеличения на 5,5 в год является подходящим кратким изложением истории, поскольку предполагает большую согласованность, чем мы видим в данных.
Нижняя диаграмма рассеяния представляет ряд проблем для типичных читателей. Прежде всего, большинство людей не знают, как интерпретировать логарифмическую шкалу. На самом деле, многие читатели могут даже не заметить, что шкала логарифмическая. Они, конечно, не будут знать, что означает наклон линии тренда, и не поймут, что эта прямая линия, наилучшим образом подходящая к логарифмической шкале, указывает на экспоненциальную скорость роста, о которой Вайнер не упоминает. Большинство читателей склонны сравнивать линии тренда и приходят к выводу, что закономерности изменений практически одинаковы. Кроме того, одно из утверждений Вайнера о данных не совсем верно:
Тенденция, сложившаяся за эти семнадцать лет, показывает, что Китай увеличивал количество активов, приобретаемых каждый год, а также приобретал все более дорогие активы.
Китай не увеличивал количество активов или количество денег, потраченных на эти активы каждый год . Есть много примеров лет, когда эти значения уменьшились, что для меня является важной частью истории.
В последнем абзаце своего объяснения Вайнер утверждает:
Основное преимущество использования парных диаграмм рассеяния с линеаризованными преобразованиями и прямыми прямыми линиями заключается в том, что они обеспечивают количественную меру того, как изменилась доходность Китая.
Это было бы только преимуществом, если бы читатели знали, как читать эти «парные диаграммы рассеяния с линеаризующими преобразованиями и прямыми прямыми линиями». К сожалению, большинство читателей этого не сделают. На самом деле, такие фразы, как «линеаризация преобразований», могут привести их в ужас.
Новость, которую New York Times пыталась рассказать, могла бы охватить все важные факты так, чтобы это было легко понять широкой аудитории. Если взаимосвязь между количеством приобретений и стоимостью этих приобретений была важна для истории, один график рассеяния, разработанный следующим образом с небольшим количеством текста для объяснения, мог бы сделать эту работу.
Я специально использовал линейные шкалы для обеих осей, чтобы линия тренда ясно демонстрировала экспоненциальный характер корреляции между двумя переменными. Я бы не стал полагаться только на график, чтобы рассказать эту часть истории, но на словах объяснил бы, что, когда линия изгибается таким образом вверх, она демонстрирует экспоненциальный темп роста: стоимость приобретений не увеличивается с приращениями, которые равны их количеству, но вместо этого увеличиваются во все большем количестве по мере увеличения числа приобретений. В дополнение к общему характеру отношений, этот график также ясно демонстрирует тот факт, что отношения несколько различаются, что особенно иллюстрируется выбросом, отклоняющимся от линии тренда в правом нижнем углу, показывая, что в конкретном году Количество приобретений не было связано с экспоненциальным увеличением затрат.
Сомнительно, что New York Times особенно интересовалась характером отношений между двумя переменными, но в основном хотела показать, как обе переменные увеличились за этот период времени. Чтобы рассказать эту историю, я бы предложил несколько дисплеев, начиная с парных линейных графиков ниже.
Это было бы легко понять обычным читателям, и оно хорошо поддерживает основное сообщение. Однако, что он делает не особенно хорошо, так это отчетливо показывает характер изменения стоимости приобретений, поскольку для масштабирования этого графика, включающего два последних чрезвычайно высоких значения, большинство значений находятся в нижних 25% шкалы. (то есть от 0 до 4 миллиардов долларов из общего масштаба, который простирается до 16 миллиардов долларов), в результате чего линия выглядит намного более плоской, чем если бы график был масштабирован для исключения двух последних значений.
Если бы этот шаблон изменений должен был отображаться более четко, и если бы мы были уверены, что наши читатели понимали логарифмические шкалы, а не отображали количество приобретений в линейном масштабе и значение приобретений в логарифмическом масштабе, шаблоны были бы более сопоставимыми если оба были масштабированы логарифмически, следующим образом.
Предположим, однако, что лучше всего избегать масштабирования журналов, чтобы избежать путаницы, что было бы в случае с общей аудиторией, даже с читателями New York Times .
Одним из потенциальных улучшений было бы поместить обе линии в один граф, но сделать это без создания запутанного и потенциально вводящего в заблуждение двумерного графика. Чтобы сделать это, мы должны выразить оба набора значений, используя одну и ту же единицу измерения и масштаб. Один из простых и распространенных способов сделать это состоит в том, чтобы выразить оба временных ряда в виде процентной разницы каждого значения по сравнению с первоначальным значением (т. Е. Значением за 1990 год). Другое распространенное выражение ценностей, которое, возможно, еще проще понять людям, заключается в выражении стоимости каждого года в процентах от общей суммы за весь период следующим образом:
Теперь, когда две линии отображаются на одном графике, их легче сравнивать. Понятно, что количество приобретений и их долларовая стоимость в этот период росли, но не всегда и не всегда вместе. Другими словами, корреляция между количеством и долларовыми суммами приобретений есть, но она не особенно сильна. Даже при том, что у нас есть проблема масштабирования, вызванная чрезвычайно высокими значениями доллара в 2005 и 2006 годах, закономерности изменений в период с 1990 по 2004 год относительно ясны и их легко сравнивать. Однако если бы это было не так, мы могли бы решить проблему масштабирования, предоставив вторую линейную диаграмму, которая включает в себя данные только с 1990 по 2004 год, а именно:
Теперь вернемся к главному. Те, кто выполняет работу по анализу данных, должны знать, как четко представлять свои выводы тем, кто полагается на эту информацию для принятия решений и принятия мер. Это важный навык. Высококвалифицированные статистики невероятно ценны, но только если они могут объяснить свои выводы в понятных терминах. Это требует навыков общения, как в использовании слов, так и в использовании графики. Обучение этим навыкам так же важно, как и обучение статистике.
Почитать еще

Введение в анализ временных рядов
Хотя для анализа данных используются все многочисленные передовые инструменты и методы, такие как наука о

История развития моделей данных
Итак, прыгайте на борт и наслаждайтесь путешествиями во времени наших попыток справиться с временностью в

Машинное обучение
Глубокое обучение – это продвинутая форма машинного обучения. Глубокое обучение относится к способности компьютерных систем, известных

Правила эффективного прогнозирования
Интуиция очень важна. С ее помощью было создано большое количество хороших прогнозов. Но нужно всегда

Выборка. Типы выборок
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков

Обзор самых популярных алгоритмов машинного обучения
Существует такое понятие, как «No Free Lunch» теорема. Её суть заключается в том, что нет

Обзор основных видов сегментации
Загрузить программу ВІ Демонстрации решений Аналитика бизнеса Оглавление Сегментация бренда Сегментация помогает принимать более эффективные

Алгоритмы машинного обучения
В одной из статей мы познакомились с основами машинного обученияи, хотя кратко, но очень лаконично, мы
Полное руководство по анализу текста
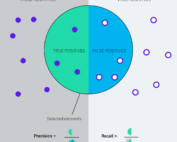
Напоминание – это количество правильных результатов, разделенное на количество результатов, которые должны были быть возвращены. Загрузить
Несколько видео о наших продуктах